how to find the radius of an arc
Arc Length
Arc length is meliorate defined as the distance along the role of the circumference of whatsoever circumvolve or any curve (arc). Any distance along the curved line that makes upwards the arc is known as the arc length. A role of a curve or a part of a circumference of a circle is called Arc. All of them take a curve in their shape. The length of an arc is longer than any straight line distance betwixt its endpoints (a chord).
| i. | What is Arc Length? |
| 2. | Arc Length Formula |
| 3. | How to Find Arc Length of a Curve? |
| 4. | FAQs on Arc Length |
What is Arc Length?
The arc length is defined equally the interspace between the ii points along a section of a curve. An arc of a circumvolve is any part of the circumference. The bending subtended past an arc at whatsoever bespeak is the bending formed between the two line segments joining that betoken to the end-points of the arc. For example, in the circle shown below, OP is the arc of the circle with center Q. The arc length of this arc OP is given as L.
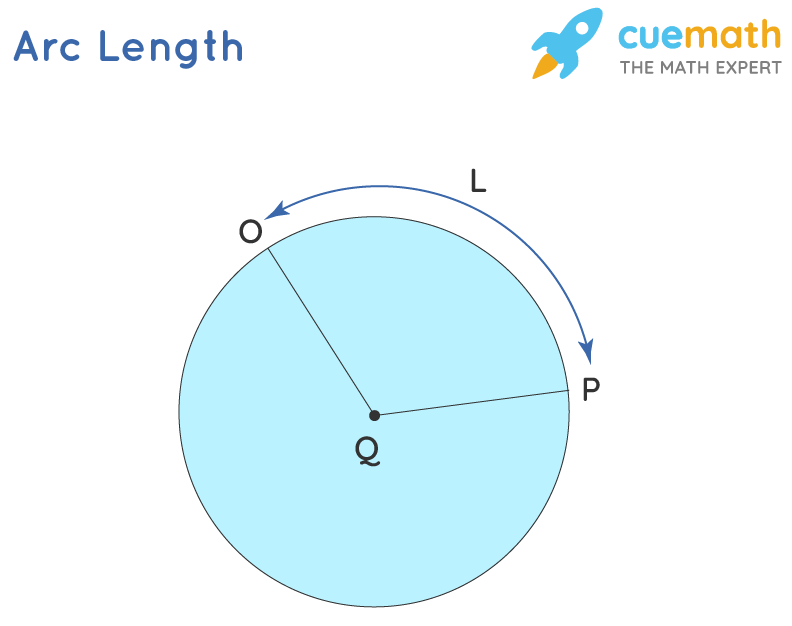
Arc Length Formula
The length of an arc can exist calculated using dissimilar formulas, based on the unit of the central angle of the arc. The measurements of the central angle can exist given in degrees or radians, and accordingly, we calculate the arc length of a circle. For a circle, the arc length formula is θ times the radius of a circumvolve.
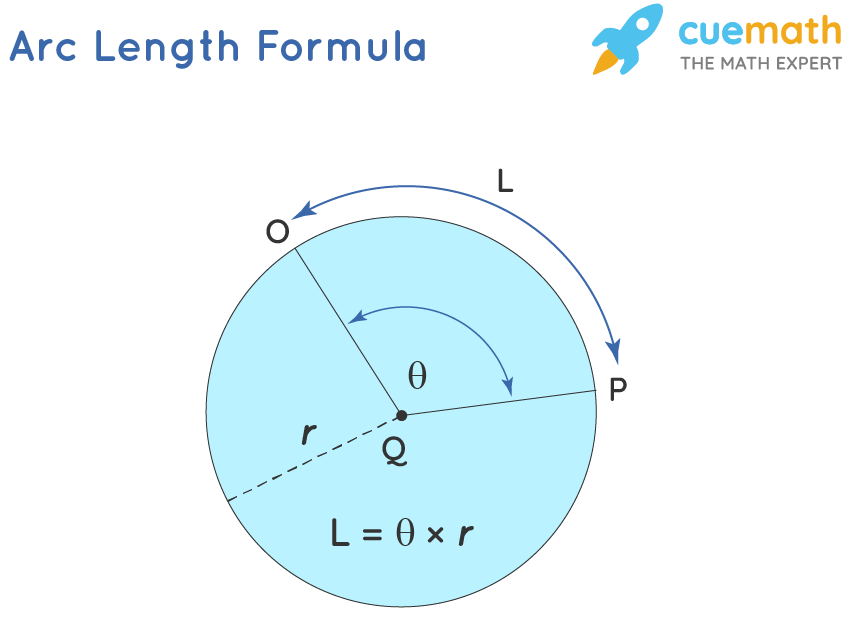
The arc length formula in radians can exist expressed as, arc length = θ × r, when θ is in radian. Arc Length = θ × (π/180) × r, where θ is in degree, where,
- L = Length of an Arc
- θ = Primal angle of Arc
- r = Radius of the circumvolve
Arc Length Formula in Radians
The arc length of a circle can be calculated using unlike formulas, based on the unit of the center angle of the arc. The arc length formula in radians tin be expressed equally,
Arc Length = θ × r
where,
- Fifty = Arc Length
- θ = Center angle of the arc in radians
- r = Radius of the circle
How to Find Arc Length of a Curve?
The arc length of an arc of a circumvolve can be calculated using different methods and formulas based on the given data. Some of import cases are given below,
- find arc length with the radius and primal bending
- find arc length without the radius
- find arc length without the primal angle
How to Detect Arc Length With the Radius and Cardinal Angle?
The arc length of a circumvolve tin can be calculated with the radius and central angle using the arc length formula,
- Length of an Arc = θ × r, where θ is in radian.
- Length of an Arc = θ × (π/180) × r, where θ is in degree.
How to Find Arc Length Without the Radius?
The arc length of a circle can be calculated without the radius using:
Key bending and the sector surface area:
- Multiply the sector surface area by two and further, dissever the upshot past the fundamental angle in radians.
- Find the square root of the event of the partition.
- Multiply this obtained root by the fundamental angle again to go the arc length.
- The units of this calculated arc length will be the square root of the sector expanse units.
Instance: Calculate the arc length of a curve with sector area 25 square units and the key angle equally 2 radians.
We have,
Sector expanse = 25 units
Central bending = ii radians
- Step ane: Sector area × ii = 25 × ii = fifty
- Step 2: 50/central angle = l/ii = 25
- Step 3: √25 = 5
- Step 4: 5 × fundamental angle = 5 × 2 = ten units
Thus, arc length = 10 units
Central angle and the chord length:
- Separate the central angle in radians by 2 and further, perform the sine function on it.
- Divide the given chord length by twice the effect of step one. This adding gives you the radius every bit result.
- Multiply the radius by the central angle to become the arc length.
Example: Calculate the arc length of a bend, whose endpoints touch a chord of the circumvolve measuring 5 units. The central bending subtended past the arc is 2 radians.
Nosotros accept,
Chord length = 5 units
Fundamental angle = 2 radians
- Step 1: Central angle/two = 2/2 = 1
- Footstep 2: Sin(one) = 0.841
- Step three:Chord length/ (2 × 0.841) = five/ 1.682 = 2.973 units = radius
- Pace iv: Arc length = radius × central angle = 2.973 × two = five.946 units
Thus, arc length = 5.946 units
How to Find Arc Length Without the Central Angle?
The arc length of a circle tin can be calculated without the bending using:
Radius and the sector area:
- Multiply the sector area by ii.
- Then divide the effect by the radius squared (the units should exist the same) to go the key angle in radians.
- Multiply the central angle by the radius to get the arc length.
Example: Summate the arc length of a curve with sector area 25 square units and radius as 2 units.
We accept,
Sector area = 25 units
Primal angle = 2 units
- Step 1: Sector area × 2 = 25 × 2 = 50
- Step 2: 50/radiusii = 50/4 = 12.5 = key angle(rad)
- Step iii: Arc length = radius × central angle = 2 × 12.5 = 25 units
Thus, arc length = 25 units
Radius and chord length:
- Divide the chord length by twice the given radius.
- Find the inverse sine of the obtained result.
- Double the outcome of the inverse sine to go the central angle in radians.
- Multiply the key bending by the radius to go the arc length.
Example: Calculate the arc length of a bend, whose endpoints touch a chord of the circle measuring five units. The radius of the circle is 2 units.
We have,
Chord length = 5 units
Central angle = 2 units
- Step ane: Chord length/(two × radius) = v/(2 × ii) = 1.25
- Step two: Sin-1(1.25) = 0.949
- Step 3: Cardinal angle = 2 × 0.949 = 1.898 radians
- Footstep four: Arc length = radius × central angle = 2 × 1.898 = 3.796 units
Thus, arc length = 3.796 units
☛ Important Notes on Arc Length
Given below are primal highlights on the concept of arc length.
- Arc Length = θ × r, where θ is in radian.
- Arc Length = θ × (π/180) × r, where θ is in degree.
☛ Related Topics on Arc Length
Check out a few more interesting manufactures related to arc length to understand the topic more precisely.
- Arc Length Computer
- Cardinal Bending
- What is a Radian?
- Arc of a Circle Figurer
- Radius
Examples on Arc length
go to slidego to slidego to slide

Breakdown tough concepts through simple visuals.
Math volition no longer be a tough subject area, particularly when y'all sympathize the concepts through visualizations.
Book a Complimentary Trial Form
Practice Questions on Arc Length
go to slidego to slide
FAQs on Arc Length
What is Arc Length of a Circle?
The arc length of a circle is defined equally the interspace between the two points along a department of a curve. An arc of a circumvolve is whatever office of the circumference. The angle subtended by an arc at any bespeak is the angle formed between the two line segments joining that bespeak to the cease-points of the arc.
How do you Notice the Length of an Arc Without the Radius?
The arc length of a circumvolve tin can be calculated without the radius using:
Primal angle and the sector area:
- Multiply the sector area by 2 and farther, divide the result by the key angle in radians.
- Find the square root of the result of the partition.
- Multiply this obtained root by the central angle over again to get the arc length.
- The units of this calculated arc length will be the square root of the sector area units.
Central angle and the chord length:
- Divide the central bending in radians past 2 and farther, perform the sine function on it.
- Divide the given chord length by twice the result of step i. This adding gives you the radius as result.
- Multiply the radius past the fundamental bending to get the arc length.
What do You lot Empathize By Arc Lenght Equation?
There are 2 equations associated with arc length. Given below are the ii arc length equations.
- Arc Length = θ × r, where θ is in radian.
- Arc Length = θ × (π/180) × r, where θ is in degree
How do yous Find Arc Length Using Radians?
The arc length can be calculated when the primal angle is given in radians using the formula: Arc Length = θ × r, when θ is in radian.
- L = Arc Length
- θ = Eye bending of the arc
- r = Radius of the circle
Does Arc Length take to be in Radians?
No, arc length cannot be in radians. It is a measurement of distance, then cannot be in radians. The central angle subtended at the center tin can be in radians, degrees, or arcsecs accordingly.
How do you lot Find the Circumference of Arc Length?
When arc length is given with central angle θ then the circumference is calculated as Arc Length (50)/Circumference = θ/360º.
What is the Length of Major Arc Using Arc Length Formula?
A major arc in a circumvolve is larger than a semicircle. It is measured as larger than 180°. Using formula ℓ = rθ we can observe the length of an arc of a circumvolve, where θ is in radian.
Source: https://www.cuemath.com/geometry/arc-length/
Posted by: reedyhadis1955.blogspot.com

0 Response to "how to find the radius of an arc"
Post a Comment